Les futures mariées sont-elles hystériques : la solution !

Snif ! Vous n’avez pas mordu à l’hameçon de mon problème de maths… Merci quand même à Maud pour son commentaire plein de bon sens, et à Julie pour ses encouragements (en fait, je lui avais déjà soumis le problème sous une forme un peu différente, et la miss a été major de sa prépa en maths donc elle ne s’est pas laissée avoir…). Comme j’ai passé un moment à rédiger la solution, la voilà quand même, et c’est assez inattendu (vous pouvez aussi sauter la démonstration et aller directement à la morale de la fable, les trois derniers paragraphes !)

Rappelons l’énoncé du problème : « Imaginons que, statistiquement, la probabilité d’être hystérique pour une femme qui n’est pas une future mariée est de 5%. Inversement, la probabilité pour une future mariée de ne pas être hystérique est de 10% seulement (la belle-mère, le gâteau, le plan de table, il y a de quoi rendre folle !). Vous rencontrez une femme complètement hystérique. Quelle est la probabilité qu’il s’agisse d’une future mariée ? »

Bridezilla -- theresa21 sur Flickr

D’expérience (en cours), la plupart des gens ont tendance 90%, ou 95%. Mais ce n’est pas forcément si simple…

Dans le monde de ce problème, une femme peut être soit hystérique, soit pas hystérique. Elle peut aussi être soit future mariée, soit pas future mariée — on pourrait se demander à partir de combien de temps avant le mariage on est considérée comme une future mariée : le moment de la demande ? Le début des préparatifs ? Plus précisément, on sait que :

– sachant qu’une femme n’est pas une future mariée, elle a 5% de chances d’être hystérique (c’est donné dans l’énoncé)

– et sachant qu’une femme n’est pas une future mariée, elle a 95% de chances de ne pas être hystérique (par déduction)

De même :

– sachant qu’une femme est future mariée, elle a 10% de chances de ne pas être hystérique (donnée)

– et, donc, 90% de chances d’être hystérique (déduction)

Si on note M l’événement « être une future mariée » et non M l’événement « ne pas être une future mariée », et qu’on note H l’événement « être hystérique » et non H l’événement « ne pas être hystérique », ceci peut se traduire par :

– Proba (H sachant non M) = 5% ou Proba (H/non M) = 5%

– Proba (non H/non M) = 95%

– Proba (non H/M) = 10%

– Proba (H/M) = 90%

Non, ne fuyez pas ! Le langage mathématique n’est ni compliqué ni effrayant, bien au contraire ! Il a été inventé par Descartes pour faciliter les démonstrations. Si vous ne me croyez pas, lisez, au hasard, le Ménon de Platon où Socrate tente d’apprendre le théorème de Pythagore à un jeune esclave, ça prend des dizaines de pages parce qu’ils n’ont pas le langage approprié. Je vous jure, le langage mathématique, c’est un progrès pour l’humanité.

Bref. Ce qu’on cherche à savoir est : sachant que la femme rencontrée est hystérique, quelle est la probabilité qu’il s’agit d’une future mariée ? On est donc en présence de l’événement H et on cherche à connaître la probabilité de M sachant H, autrement dit Proba (M/H).

C’est là qu’intervient un matheux nommé Bayes, connu des élèves de terminale. Il nous dit que Proba (M inter H) = Proba (M/H) x Proba (H), où M inter H désigne l’intersection de M et H, à savoir la probabilité qu’une femme soit à la fois hystérique et future mariée : elle est égale à la probabilité qu’une femme soit hystérique, fois la probabilité qu’elle soit future mariée sachant qu’elle est hystérique.

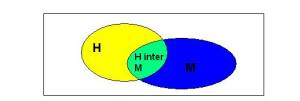Autrement dit  : la probabilité de l’aire verte (l’intersection) est égale à la probabilité de l’aire jaune (H) fois la probabilité d’être dans le morceau vert sachant qu’on est dans l’aire jaune. Ou, au choix, dans l’autre sens : la probabilité de l’aire bleue (M) fois la probabilité d’être dans le morceau vert sachant qu’on est dans l’aire bleue.

Puisque Proba (M inter H) = Proba (M/H) x Proba (H), on peut diviser les deux côtés de l’équation par Proba (H), et on obtient : Proba (M/H) = Proba (M inter H) / Proba (H).

Héhé ! Mais la proba de (M/H), c’est justement ce qu’on cherche ! On va donc pouvoir le calculer ! Pour ça il nous faut donc Proba (M inter H) et Proba (H).

– Proba (M inter H), c’est facile : en utilisant la formule de Bayes, on peut écrire Proba (M inter H) = Proba (H/M) x Proba (M) au lieu de Proba (M/H) x Proba (H), qu’on avait utilisé plus haut.

Or, on connaît Proba (H/M) : c’est 90%, on l’a déduit de l’énoncé : sachant qu’une femme est future mariée, elle a 90% de chances d’être hystérique. Proba (M), voilà plus épineux. Quelle est la probabilité qu’une femme soit future mariée dans la population en question ? L’énoncé est muet à ce sujet. Disons que cette probabilité est de α, on arrivera peut-être à la trouver plus tard. Proba (M inter H) est alors 0,9 α.

– Peut-on tout de même calculer Proba (H) ? Eh bien, sachant qu’il y a des hystériques à la fois chez les futures mariées et chez celles qui ne le sont pas, l’événement H se décompose en H inter M (être hystérique et future mariée) et H inter non M (être hystérique et pas future mariée). Les deux sont distincts (on ne peut pas être à la fois future mariée et pas future mariée), donc on peut les additionner et dire que Proba (H) = Proba (H inter M) + Proba (H inter non M).

D’après Bayes, toujours lui, Proba (H inter M) = Proba (M) x Proba (H/M) soit Proba (M) x 90%, ce qui équivaut à 0,9 α.

De même, Proba (H inter non M) = Proba (non M) x Proba (H/non M). Comme M et non M sont complémentaires (on est soit M, soit non M), Proba (non M) = 1 – Proba (M), soit 1 – α. Et proba (H/non M) = 5%, d’après l’énoncé. Donc Proba (non M) x Proba (H/non M) = 0,05 x (1 – α).

Donc Proba (H) = 0,9 α + 0,05 x (1 – α)

Récapitulons :

La probabilité que nous cherchons est Proba (M/H). D’après Bayes, Proba (M/H) = Proba (M inter H) / Proba (H). Or : Proba (M inter H) = 0,9 α. Et Proba (H) = 0,9 α + 0,05 x (1 – α). Alors Proba (M/H) = 0,9 α / (0,9 α + 0,05 x (1 – α)), ou encore 0,9 α / (0,9 α + 0,05 – 0,05 α), soit 0,9 α / (0,85 α + 0,05).

Impossible de résoudre le problème sans connaître α, c’est-à-dire la probabilité qu’une femme soit une future mariée !

Oui, bon, vous allez peut-être vous dire que je vous casse les pieds avec mon problème de maths… Mais un exemple va montrer pourquoi ça peut être important…

Imaginons qu’il y ait 10 000 femmes. 100 d’entre elles sont de futures mariées, ce qui représente 1% de la population. Il y en a donc 9 900 qui ne sont pas de futures mariées. D’après notre énoncé :

– 10% des futures mariées ne sont pas hystériques, ce qui fait 10 personnes (10% de 100).

– 90% des futures mariées sont hystériques, soit 90 personnes.

– 5% des femmes qui ne vont pas se marier sont hystériques, soit 495 personnes (5% de 9 900).

– 95% des femmes qui ne vont pas se marier ne sont pas hystériques : 9 405 personnes.

. Parmi les hystériques, il y a donc 90 futures mariées et 495 femmes qui ne sont pas des futures mariées. Donc, si on tombe sur une hystérique, la probabilité que ce soit une future mariée est de 90 / (90 + 495) = 90 / 585 = 15,4%.

Donc : la probabilité d’avoir affaire à une future mariée est plus élevée si la personne est hystérique (15,4% de futures mariées parmi les hystériques) que si vous prenez une personne au hasard dans la population (1% de futures mariées dans la population totale). Mais pas forcément aussi élevée qu’on pourrait croire… Tout dépend de la proportion de futures mariées dans la population étudiée…

Et pourtant, nous commettons ce genre d’erreur tous les jours. C’est même la base de nombreux préjugés. Par exemple : 90% des meilleurs joueurs de squash sont pakistanais. Vous êtes à un tournoi de squash et votre adversaire est pakistanais. Est-il pour autant un bon joueur ? On n’en sait rien. Tout ce qu’on peut dire, c’est qu’il a plus de chances d’être un bon joueur que s’il n’était pas pakistanais, mais on ne peut rien en déduire de précis…

(et voilà, bienvenue dans le monde merveilleux de la probabilité conditionnelle ! qui a dit qu’on ne pouvait parler que de futilités en été ?)

Les futures mariées sont-elles toutes hystériques ?

Dans les films américains, on reconnaît la future mariée à son obsession du jour J, ses caprices incessants, et souvent, il faut bien le dire, au fait qu’elle soit complètement hystérique. Bridezilla…

Mais les futures mariées sont-elles toutes dans ce cas ? Et, plus important pour nous tous qui voulons nous prémunir de la bridezilla, l’hystérie est-elle un bon indicateur qu’on a affaire à une future mariée ?

Imaginons que, statistiquement, la probabilité d’être hystérique pour une femme qui n’est pas une future mariée est de 5%. Inversement, la probabilité pour une future mariée de ne pas être hystérique est de 10% seulement (la belle-mère, le gâteau, le plan de table, il y a de quoi rendre folle !). Vous rencontrez une femme complètement hystérique. Quelle est la probabilité qu’il s’agisse d’une future mariée ?

(Je vous laisse chercher un peu, réponse lundi !)